Amélioration d'un crontab
Analyse stats & amélioration d'un crontab
Récemment j'ai travaillé sur l'amélioration d'un serveur Linux qui exécutait des centaines de crontab. J'ai cherché à améliorer les performances.
Le problème était que les scripts étaient exécutés en même temps, ce qui saturait le serveur.
(Souvent on utilise des crontab avec des intervalles de temps fixe, ce qui peut causer des problèmes de saturation).
Distribution des exécutions des scripts
On peut voir que la distribution des exécutions des scripts est assez hétérogène.
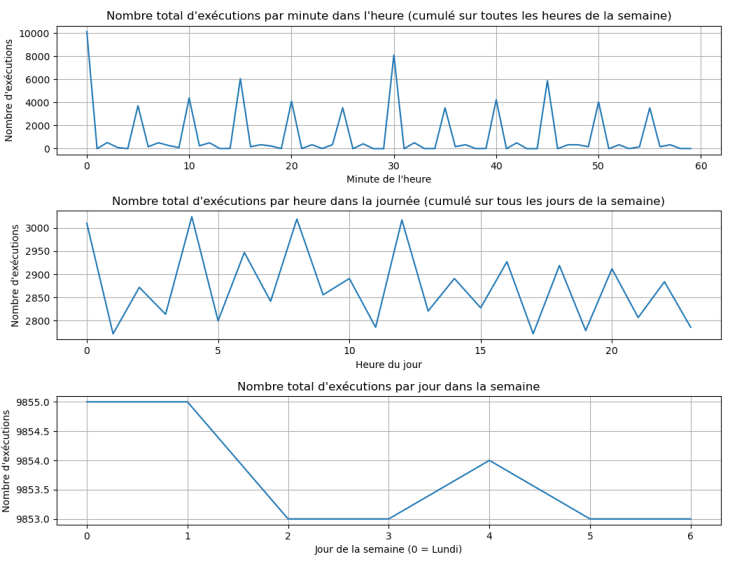
Figure 1: Distribution des exécutions cumulée des scripts par minutes, heures, jours
En figure 1, on peut voir des pics sur des intervalles fixe. Tel que 0, 5, 10, 15, 20... minutes.
On va maintenant regarder spécifiquement la variation de la distribution des exécutions cumulée des scripts par minutes dans l'heure.
C'est-à-dire comment les scripts sont répartis dans l'heure (pour voir s'il y a beaucoup de script dans la même minute).
Pour faire cela on calcule la dérivée temporelle du nombre de scripts exécutés par minutes, ensuite on calcule une régression gaussienne:
Soit $g_n$ suite numérique des données d'index $n$. La dérivée est: $$\Delta g_n = g_{n+1} - g_n$$
Ou bien en continu (avec $g(n)$ la fonction):
$$(E_1): \frac{d}{d n} g(n) = \lim_{\delta n \to 0} \frac{g(n + \delta n) - g(n)}{\delta n}$$
Comme $g_n \vcentcolon= g(n) \forall n \in \N$ : $d n=\delta n$.
$$(E_1) \Rightarrow d g = \lim_{\delta n \to 0} g(n + \delta n) - g(n)$$
$d g$ est calculé avec numpy.diff.
Ainsi ici: $$\Delta g_n = d g(n)$$
On vient de montrer que l'on peut calculer la dérivée avec une différentielle discrète (donc avec
numpy.diff).
Soit notre gaussienne: $$f(x) = a \exp\left(-\frac{(x - b)^2}{2c^2}\right)$$ (avec $a$ l'amplitude, $b$ la moyenne et $c$ l'écart-type)
On cherche à ajuster la gaussienne à la dérivée: $$\min_{a, b, c} \sum_{n=0}^{N-1} \left(\Delta g_n - f(n)\right)^2$$
On fait cette minimisation avec la méthode de scipy (Méthode du maximum de vraisemblance).
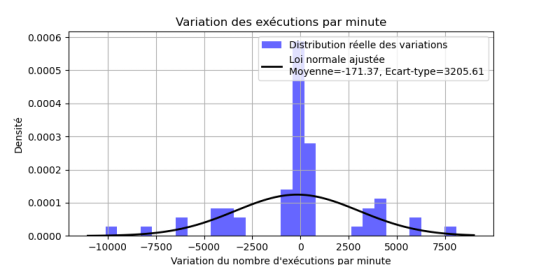
Figure 2: Variation de la distribution des exécutions des scripts par minutes dans l'heure
On a une variation moyenne de -171 scripts exécutée par minutes par heure, avec un écart-type de 3205.
Solution
Pour réduire le chevauchement, on peut légèrement décaler les scripts qui sont exécutés à la même minute.
J'ai donc réalisé une simulation pour voir l'impact de ce décalage:
- J'ai décalé les scripts de plus ou moins 2 minutes aléatoirement.
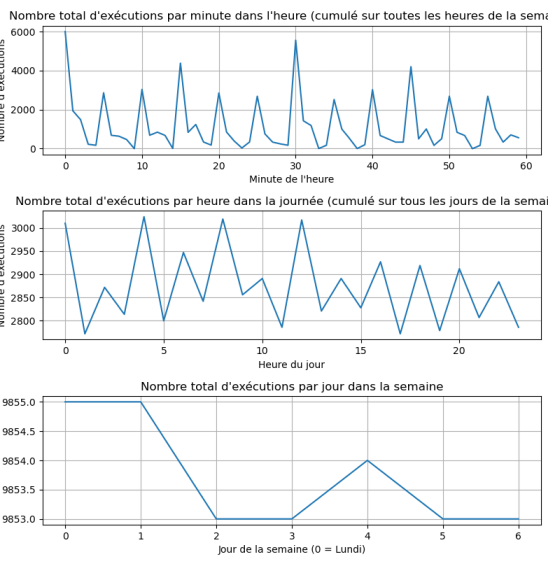
Figure 3: Distribution des exécutions cumulée des scripts par minutes, heures, jours avec décalage de 2mins
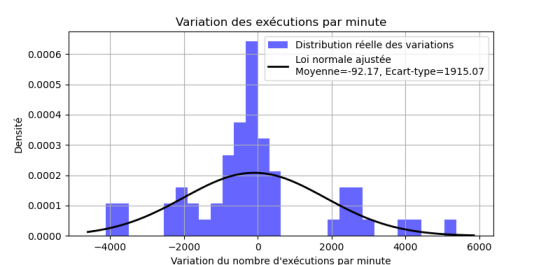
Figure 4: Variation de la distribution des exécutions des scripts par minutes dans l'heure avec décalage
On peut voir que le chevauchement est réduit, mais il reste encore des chevauchements, nous avons réduit la variation moyenne à -92 scripts exécuté par minutes par heure, avec un écart-type de 1915.
NB: L'idéal serait une valeur moyenne nulle et un écart-type faible.
On peut encore lisser la distribution en décalant les scripts de plus ou moins 3 minutes aléatoirement.
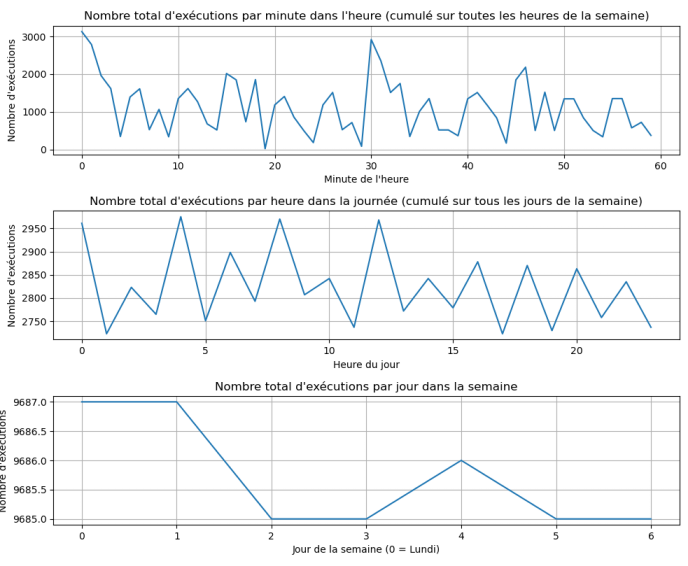
Figure 5: Distribution des exécutions cumulée des scripts par minutes, heures, jours avec décalage de 3mins
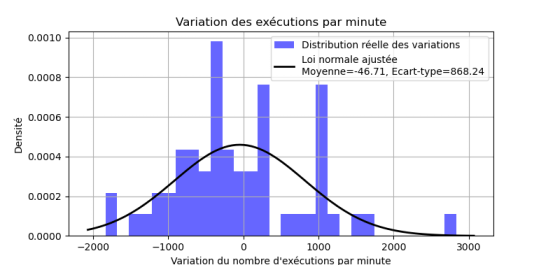
Figure 6: Variation de la distribution des exécutions des scripts par minutes dans l'heure avec décalage de 3mins
Paramètres de la loi normale ajustée (variation) : Moyenne = -46.7, Écart-type = 868.2
ATTENTION: Si on augmente trop le décalage, on risque de décaler les scripts qui sont dépendants les uns des autres.
Mais également, cela peut revenir à un chevauchement des scripts à une autre minute:
Par exemple avec un décalage de 10 minutes, les performances sont moins bonnes: Moyenne = -60.1, Écart-type = 1376.0
Ainsi on a réussi à lisser la distribution des exécutions des scripts dans l'heure.
Résultats d'un lissage sur 3 minutes:
- Moyenne: passage de -171 à -46.7
- Écart-type: passage de 3 205 à 868.2
- Nombre de scripts exécutés en même temps au maximum passé de plus de 1 500 à 430 (moyenne sur 7 jours) (Réduction de 71.4%).
Recherche du shift optimal
Comme le script de décalage est aléatoire, on va lancer 9 simulations pour chaque décalage de 1 à 10 minutes.
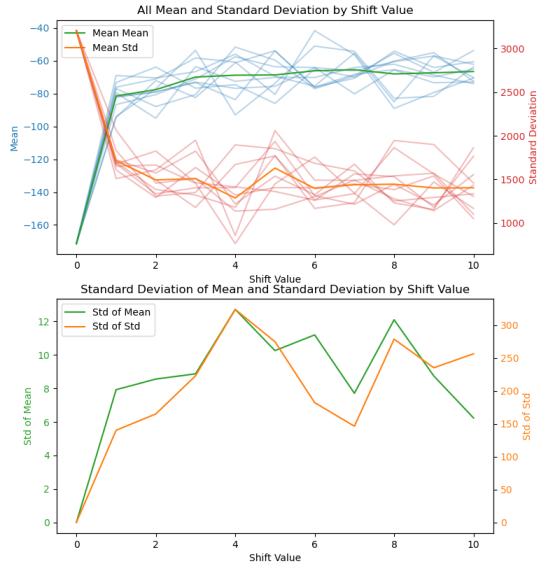
Figure 7: Variation de la distribution des exécutions des scripts par minutes dans l'heure avec décalage de 1 à 10mins moyenné sur 9 essais
Annexes
Code pour décaler les crontabs
import random
from croniter import croniter
from datetime import datetime, timedelta
SHIFT = 10
def shift_crontab(crontab):
"""Décale aléatoirement les minutes d'une crontab de -2 à +2 minutes, y compris les plages et intervalles."""
parts = crontab.split()
# On modifie uniquement la première partie, qui correspond aux minutes
minute = parts[0]
# Si c'est une étoile avec un intervalle, comme */15 ou 2-59/15
if '*/' in minute or '-' in minute:
if '*/' in minute:
interval = int(minute.split('/')[-1])
shift = random.randint(-SHIFT, SHIFT)
new_minute = f"*/{interval}" if shift == 0 else f"{max(0, shift)}-{min(59, 60-shift)}/{interval}"
elif '-' in minute:
# Si c'est un intervalle avec un range comme 2-59/15
range_part, step = minute.split('/')
start, end = map(int, range_part.split('-'))
shift = random.randint(-SHIFT, SHIFT)
start = (start + shift) % 60
end = (end + shift) % 60
start = max(0, start) # S'assurer que start ne descend pas sous 0
end = min(59, end) # S'assurer que end ne dépasse pas 59
new_minute = f"{start}-{end}/{step}"
parts[0] = new_minute
# Si ce sont des minutes exactes comme 0,4,8,10
elif ',' in minute:
new_minutes = []
for m in minute.split(','):
if m.isdigit():
minute_value = int(m)
shift = random.randint(-SHIFT, SHIFT)
new_minute = (minute_value + shift) % 60
new_minutes.append(str(new_minute))
parts[0] = ','.join(new_minutes)
# Si c'est une valeur fixe de minute comme "0", "30", etc.
elif minute.isdigit():
minute_value = int(minute)
shift = random.randint(-SHIFT, SHIFT)
new_minute = (minute_value + shift) % 60 # Gérer l'overflow des minutes (0-59)
parts[0] = str(new_minute)
return ' '.join(parts)
def shift_crontab_list(crontab_list):
"""Applique un décalage aléatoire de minutes sur une liste de crontabs."""
shifted_crontabs = []
for crontab in crontab_list:
shifted_crontab = shift_crontab(crontab)
shifted_crontabs.append(shifted_crontab)
return shifted_crontabs
Code pour simuler un lancement de crontabs (1 semaine)
def generate_execution_dates(crontab_list, start_time, end_time):
"""Génère toutes les dates d'exécution pour chaque crontab entre start_time et end_time."""
execution_dates = []
for cron_expr in crontab_list:
cron = croniter(cron_expr, start_time)
while True:
next_execution = cron.get_next(datetime)
if next_execution >= end_time:
break
execution_dates.append((cron_expr, next_execution))
# Trier la liste des exécutions par date
execution_dates.sort(key=lambda x: x[1])
return execution_dates
def generate_weekly_schedule(crontab_list):
"""Génère toutes les dates d'exécution pendant une semaine à partir de la liste des crontab."""
#now = datetime.now().replace(second=0, microsecond=0, minute=0, hour=0) # Début de la journée
#Start from 14/10/24
now = datetime(2024, 10, 14, 0, 0, 0)
start_time = now
end_time = start_time + timedelta(weeks=1) # 1 semaine plus tard
end_time = end_time.replace(second=0, microsecond=1, minute=0, hour=0) # Fin de la journée
# Bien mettre microsecond=1 pour prendre en compte les dates exactes (0.999999999 != 1 en info)
execution_dates = generate_execution_dates(crontab_list, start_time, end_time)
return execution_dates
Code pour lire la simulation depuis un fichier
# Fonctions pour compter les exécutions (précédentes)
def parse_weekly_schedule(filename):
"""Parse le fichier weekly_schedule.txt pour obtenir la liste des exécutions."""
with open(filename, 'r') as f:
lines = f.readlines()
execution_dates = []
for line in lines:
execution_dates += [datetime.strptime(line.strip(), '%Y-%m-%d %H:%M:%S')]
return execution_dates
Code pour calculer la distribution des exécutions par minutes
def executions_per_minute(execution_dates):
executions_per_minute = [0] * 60
for exec_date in execution_dates:
executions_per_minute[exec_date.minute] += 1
return executions_per_minute
# Fonction pour tracer la dérivée (variation) et ajuster une loi normale
def plot_variation_distribution_and_fit(data, title, xlabel):
"""Trace la distribution de la variation (dérivée) des données et ajuste une loi normale."""
plt.figure(figsize=(8, 6))
# Calcul de la variation (dérivée)
variation = np.diff(data)
# Calcul de la distribution de la variation
count, bins, ignored = plt.hist(variation, bins=30, density=True, alpha=0.6, color='b', label='Distribution réelle des variations')
# Ajustement de la loi normale
mu, std = norm.fit(variation)
# Générer la courbe de la loi normale pour la variation
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, std)
plt.plot(x, p, 'k', linewidth=2, label=f'Loi normale ajustée\nMoyenne={mu:.2f}, Ecart-type={std:.2f}')
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel('Densité')
plt.legend()
plt.grid(True)
plt.show()
# Affichage des paramètres ajustés
print(f"Paramètres de la loi normale ajustée (variation) : Moyenne = {mu}, Écart-type = {std}")
executions_minute = executions_per_minute(execution_dates)
plot_variation_distribution_and_fit(executions_minute, 'Variation des exécutions par minute', 'Variation du nombre d\'exécutions par minute')