Étude des systèmes GNSS des smartphones
Étude des systèmes de navigation par satellite global appliquée aux smartphones
Ce post est issu de mon TIPE de CPGE, https://github.com/n005/tipe_beamer (réalisé en 2023).
Introduction
Je vais décrire dans ce post mon TIPE de CPGE, qui porte sur l'étude des systèmes de navigation par satellite global (GNSS) appliqué aux smartphones.
En effet, les smartphones sont de plus en plus équipés de puces GNSS, et il est intéressant de comprendre comment ces systèmes fonctionnent, et comment ils peuvent être améliorés.
Nous avons un besoin croissant de géolocalisation précise, notamment pour les applications de cartographie, de guidage, ou encore de réalité augmentée, ce besoin est grandissant:
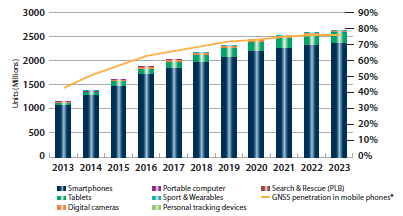
Définition GNSS
Le GNSS est un système de navigation par satellite global, qui permet de déterminer la position d'un récepteur sur Terre, en utilisant des satellites en orbite. GNSS: Global Navigation Satellite System (Système de navigation par satellite global)
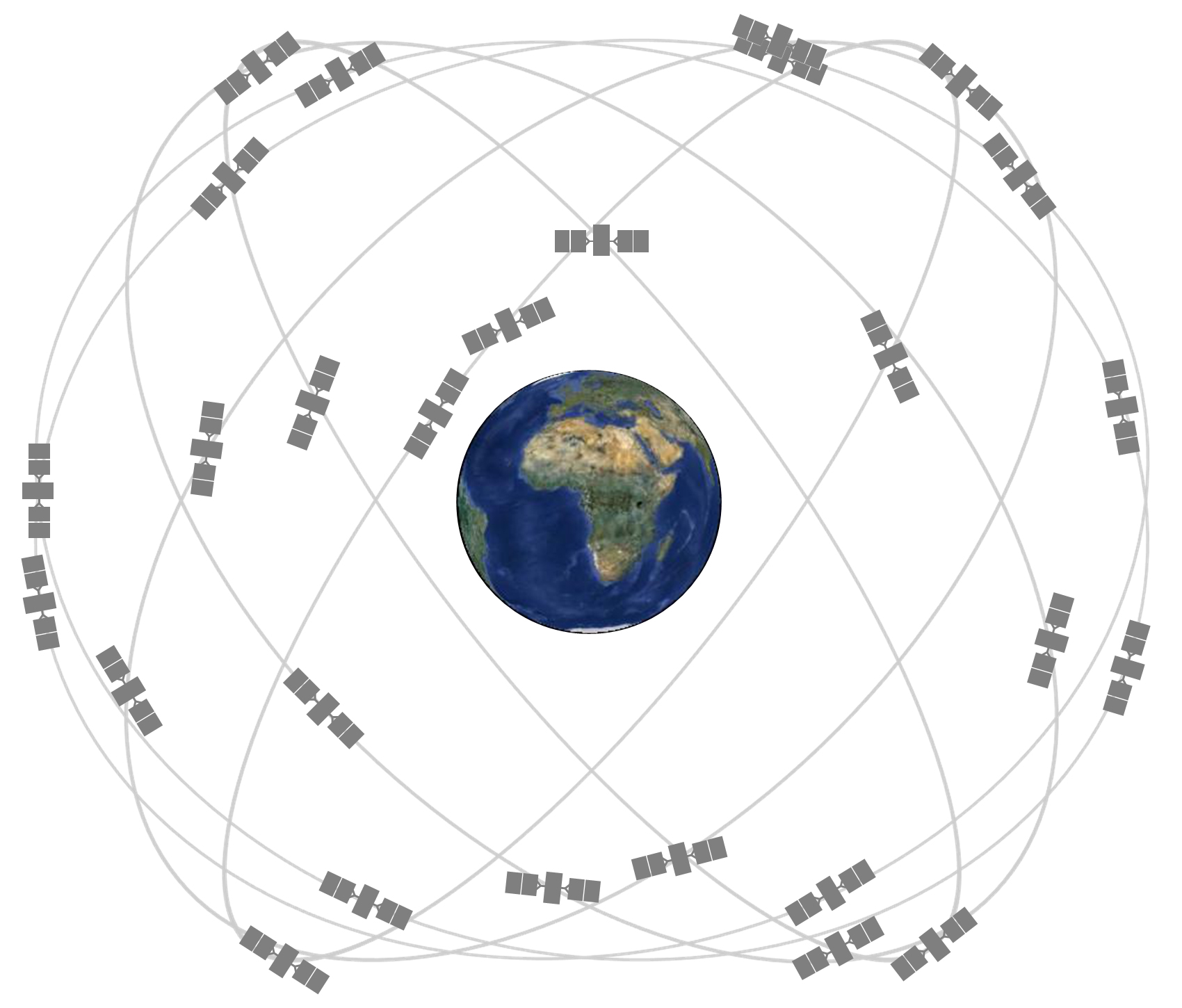
Fonctionnement du GPS
Le fonctionnement du GPS est basé sur la mesure du temps de propagation du signal émis par les satellites, et la triangulation de la position du récepteur.
Il s'agit de résoudre une équation de la forme suivante:
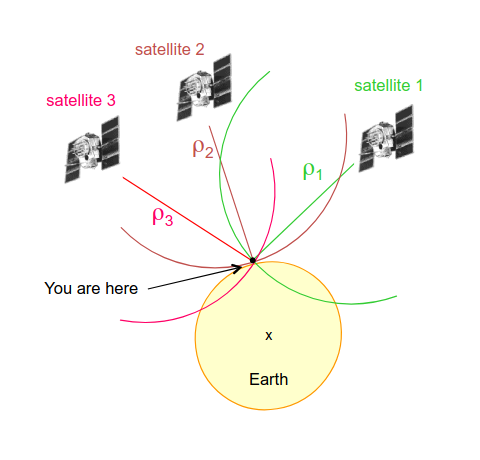
Une sphère de rayon $\rho_1 = (\Delta t_1 \cdot c)$
3 satellites, intersection des 3 sphères. Et donc
$\rho_s^s = \sqrt{(X^s-X_r)^2 + (Y^s-Y_r)^2 + (Z^s-Z_r)^2}$
Avec:
-
$X^s, Y^s, Z^s$ : coordonnées du satellite $s$ ;
-
$X_r, Y_r, Z_r$ : coordonnées du récepteur.
Sources d’incertitude
Néanmoins le modèle précédent est simplifié, et ne prend pas en compte toutes les sources d'incertitude qui peuvent affecter la précision de la géolocalisation:
- Les horloges des satellites et des récepteurs ne sont pas synchronisés. ($\delta t$) (Exemple Annexe 6)
- Réfraction lors de la propagation dans l’atmosphère :
- Troposphérique ($T_r^s$)
- Ionosphérique (dépend de la densité ionique) ($I_r^s$)
Modèle plus complet : $$\boxed{R_r^s = \rho_r^s + c\delta t + T_r^s + I_r^s + ...}$$
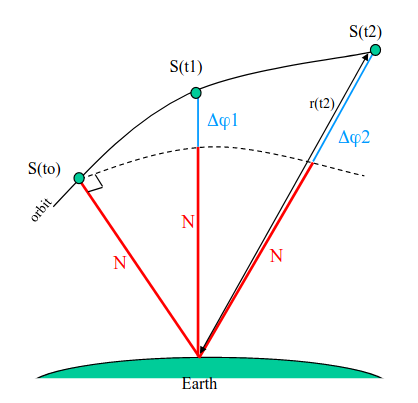
Précision des orbites
Les systèmes GNSS sont basés sur des orbites prédites émises par les
satellites.
Elles permettent de connaître la position des satellites à un instant donné.
Ces éphémérides doivent donc être très précises.
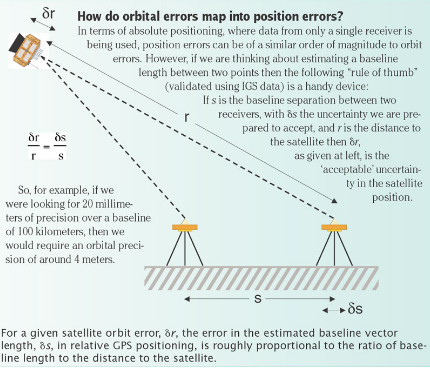
L'image explique l'intérêt de la précision des orbites, et l'impact sur la précision de la géolocalisation. (Nous devons avoir une précision orbitale de l'ordre de 4 mètres pour une précision de 20 mm sur Terre.)
Il existe aussi des services qui recalculent les éphémérides apostériori. (eg. IGN). Ces services permettent de corriger les erreurs d'orbite, et donc d'améliorer la précision de la géolocalisation.
Multipath et dilution
Une autre source d'erreur est le multipath, qui est la réflexion du signal sur des obstacles avant d'atteindre le récepteur.
Cela peut entraîner des erreurs de plusieurs mètres, et affecter la précision de la géolocalisation.
La dilution géométrique est un autre facteur qui influe sur la précision. Elle dépend de la géométrie des satellites, et peut augmenter l'erreur de positionnement.
Le multipath (multi-trajet): le signal émis par le satellite est réfléchi avant d’atteindre le récepteur. (cf. Figure 1)
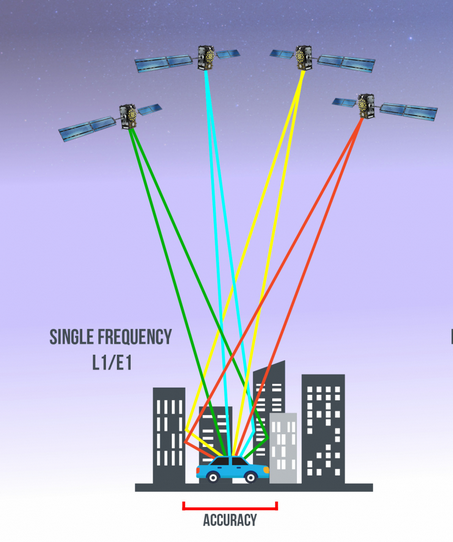
La dilution (GDOP): la géométrie des satellites influe sur la précision. (cf. Figure 2)
Problématique
Comment peut-on réduire l’impact de l’urbanisation sur les systèmes GNSS pour améliorer la précision de la géolocalisation par satellite ?
Objectifs
-
Impact de l’ionosphère et des corrections possibles.
-
Étude du multipath, dilution géométrique, GPS à doubles fréquences.
-
Comparaison Ville / campagne de la précision.
L’ionosphère
Définition
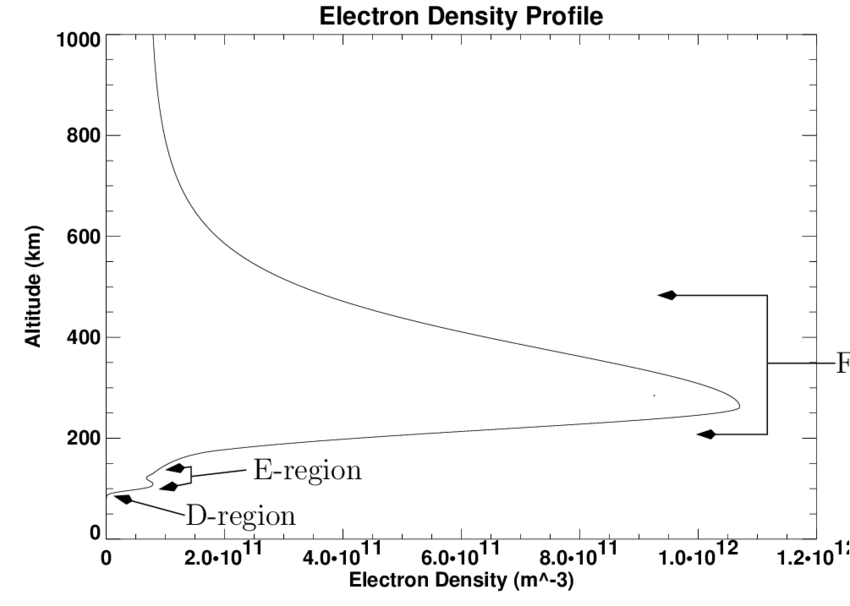
L’ionosphère : Située entre 60 et 1000 km d’altitude.
Constituée de particules chargées électriquement, les ions, en
mouvement.

Impact sur la propagation
L'ionosphère a un impact sur la propagation des ondes GNSS, en particulier sur la phase et la pseudorange.
En effet, les ondes peuvent être réfractées par l'ionosphère.
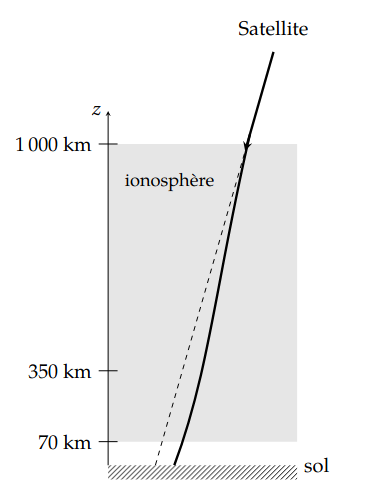
Impact sur la propagation :
-
Propagation directe - Sans interaction avec l’ionosphère.
-
Propagation réfractée - Avec interaction avec l’ionosphère.
Indice :
$$ n=1- \frac{f_p^2}{2f^2} < 1 $$
(Voir annexe 2)
Quelle erreur ?
L'erreur due à l'ionosphère peut être importante, et peut atteindre plusieurs mètres. Regardons un exemple de calcul de l'erreur due à l'ionosphère:
Milieu Linéaire, Isotrope, transparent, inhomogène
Retard Ionosphérique :
$\tau = \frac{1}{c} \int_{0}^{H_0} (\frac{c}{v_g}-1)$
Erreur de distance :
$L = \frac{a}{f_1^1} C_{ET}$ avec $C_{ET} = \int_{0}^{H_0} n_e dz$
(Contenu Électronique Total)
A un TEC de $1.5\cdot 10^{17} m^{-2}$ $$ \boxed{L = 220m} $$
Pour calculer on a donc besoin de la phase et de la pseudorange sur deux fréquences. (Voir Annexe 2)
On observe 220m d'erreur possible théorique.
Afin de calculer le TEC, un récepteur Dual-Band (L1, L5) est nécessaire :
Un récepteur dual-band permet de recevoir des informations du même satellite sur deux fréquences différentes.
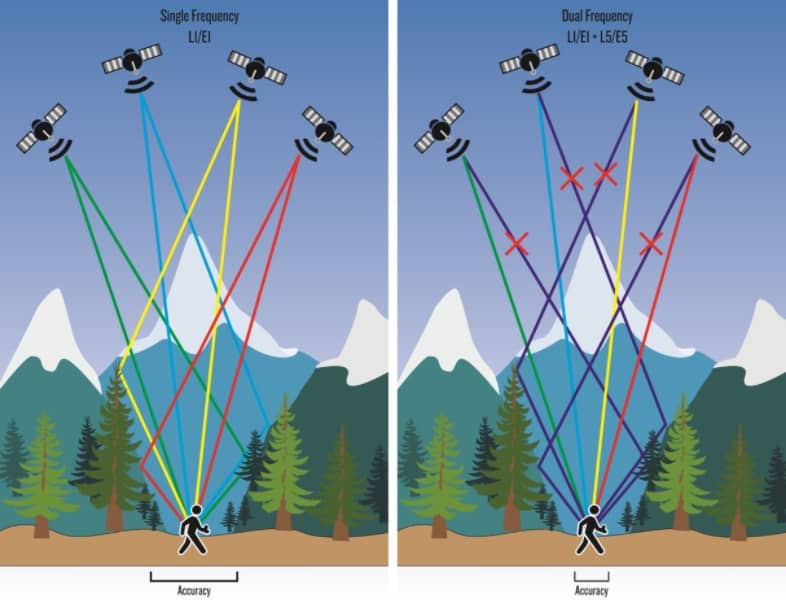
Désormais disponible dans les smartphones(depuis 2018):

On peut donc mener des expérimentations pour évaluer l'impact de l'ionosphère sur la géolocalisation.
Expérimentations Ionosphérique
Nous allons réaliser des expérimentations pour évaluer l'impact de l'ionosphère sur la géolocalisation, en utilisant un smartphone capable de recevoir en dual-band.
Méthode d’évaluation: Le retard s’évalue grâce à un même signal sur deux fréquences.
Le signal GPS:
-
Pseudorange - La pseudorange (distance) s’évalue à l’aide d’une fonction de corrélation.
-
Phase - La phase s’évalue sur le nombre de phases depuis le début d’acquisition. (Voir Annexe 3)
Il est possible de connaître l’état de l’ionosphère (indice Kp).
Protocole expérimental
Pour réaliser nos expériences, nous allons utiliser un smartphone capable de recevoir en dual-band:
- Récupération des données brute sur Xiaomi Mi 8 avec GNSS Logger de Google.
- Calcul du délai ionosphérique avec Python (Voir Annexe 7).

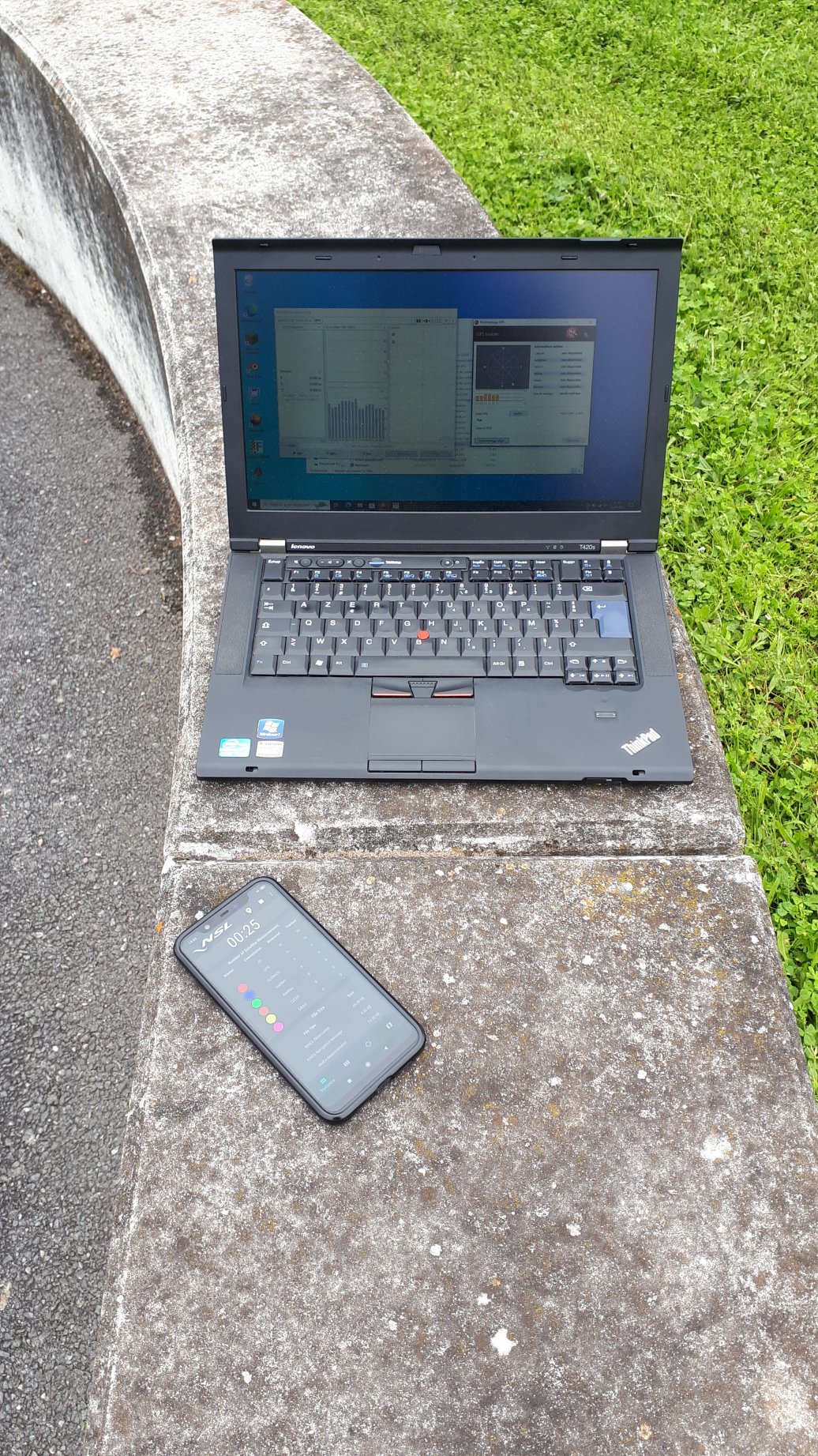
Contexte
Voici le contexte d'une session d'expérimentation, avec le ciel visible et les signaux reçus.


Contexte - Signal sur bruit
Nous pouvons dans un premier temps évaluer le signal sur bruit, qui est un indicateur de la qualité de la réception, et de la perturbation du signal. (Présence d'obstacle, réflexion, etc.)
Signal sur bruit :
-
Rapport entre la puissance du signal et la puissance du bruit.
-
$SNR = 10 \cdot log_{10}(\frac{P_{signal}}{P_{bruit}})$

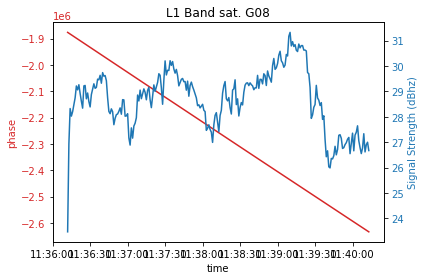
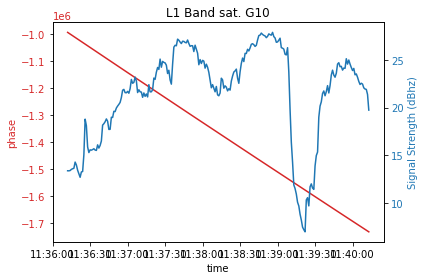
Résultats
L’estimation du délai n’est possible que sur de courte session due aux duty cycle (Voir Annexe 3)
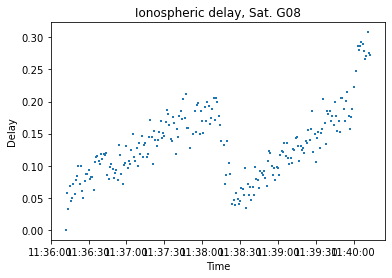
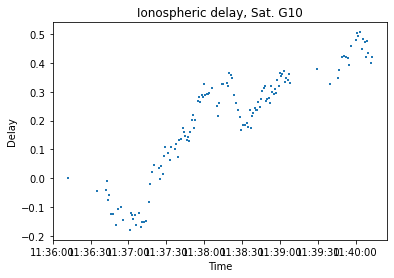
Multipath
Nous allons maintenant nous intéresser à une autre source d'erreur, le multipath, qui est la réflexion du signal sur des obstacles avant d'atteindre le récepteur.
Multipath
Multipath : Plusieurs trajets entre l’émetteur et le récepteur d’une même onde. Le multipath s’estime par :
$$ MP = P - (\frac{2}{\alpha - 1} + 1) \cdot L_1 + \frac{2}{\alpha - 1} \cdot L_2 $$
avec $P$ la phase, $L_1$ la pseudorange, $L_2$ la pseudorange sur la deuxième fréquence et $\alpha$ le coefficient de réflexion.
(Voir Démonstration Annexe 4)
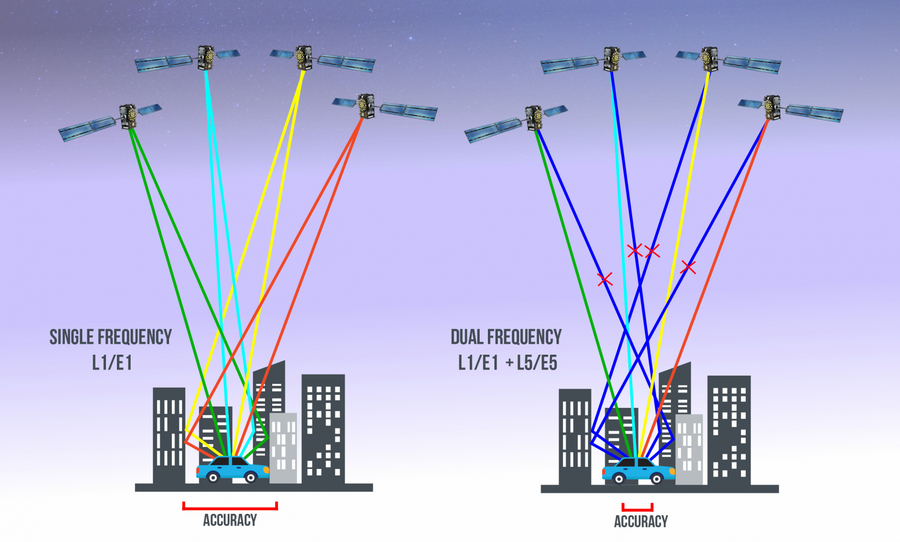
Besoin de connaître la phase et de la pseudorange sur deux fréquences.
Quelle erreur ?
Le multipath peut entraîner des erreurs de plusieurs mètres, et affecter la précision de la géolocalisation.
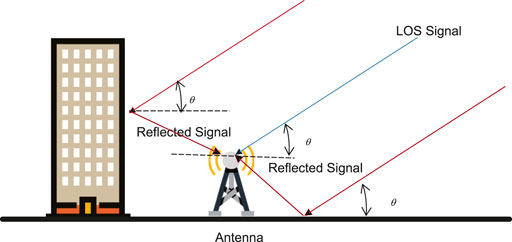
L’erreur est de plusieurs mètres. (Serrano, Kim, and Langley 2008)
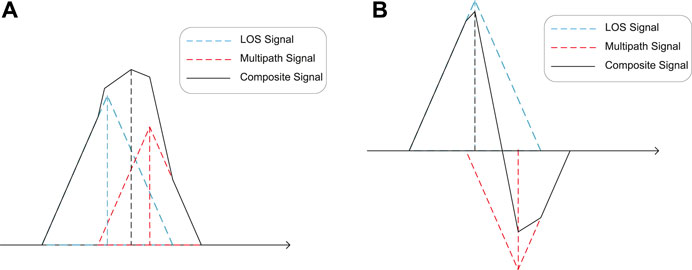
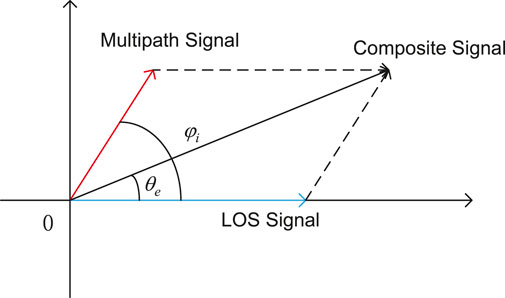
Expériences sur le Multipath
Protocole expérimental
-
Calcul du multipath à partir de la phase et de la pseudorange.
-
Basé sur un article de Umberto et al. (Robustelli, Baiocchi, and Pugliano 2019)
-
Utilisation d’un Xiaomi Mi 8 et de Google GNSS Logger pour récupérer les fichiers RINEX. (voir Annexe 5)
-
Deux cas: peu de réflexion (campagne) et beaucoup de réflexion (ville).
-
Traitement des données avec rtklib. (Conversion de format)
-
Traitement et calcul du multipath avec Tecq.
-
Analyse des résultats avec Python. (Voir Annexe 7)
-



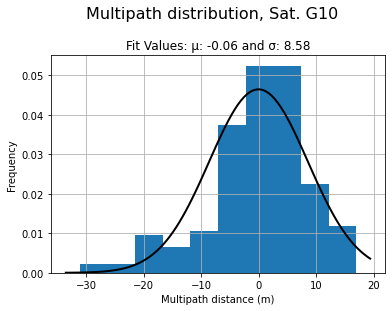
Résultats Erreur multipath en ville et en campagne:
En ville, on a une erreur de 2.5 mètres en moyenne. (Robustelli, Baiocchi, and Pugliano 2019)
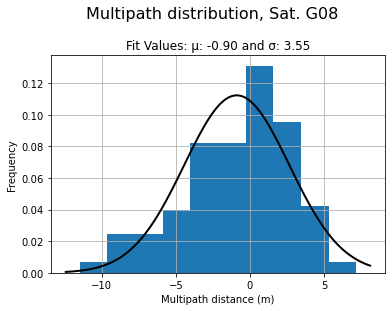
En campagne, l’erreur est de quelques dizaine de centimètres. (Robustelli, Baiocchi, and Pugliano 2019)
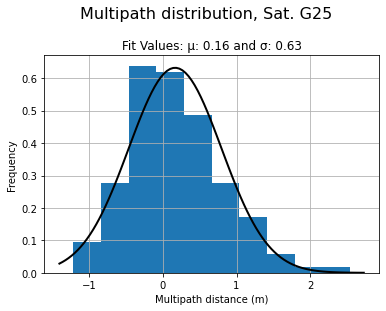
Cela s'explique par le fait qu'en ville, il y a plus d'obstacles et de réflexions, ce qui entraîne une plus grande erreur.
Corrections
Avec RTKlib:
Sans correction liée à la double fréquence (soit, ionosphère et
multitrajets)
Uniquement sur le code (pseudorange)
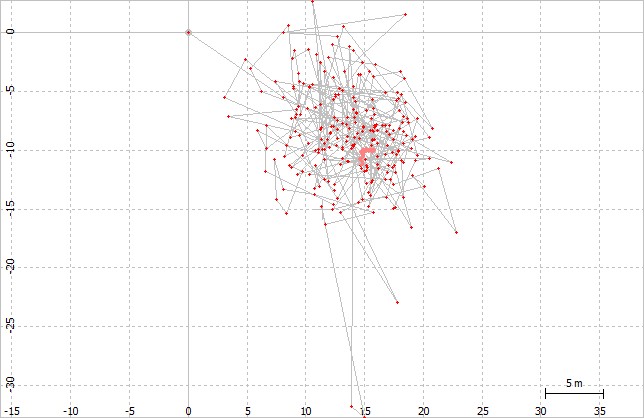
Avec correction liée à la double fréquence. (ESA, n.d.a)
Sur pseudorange et phase.
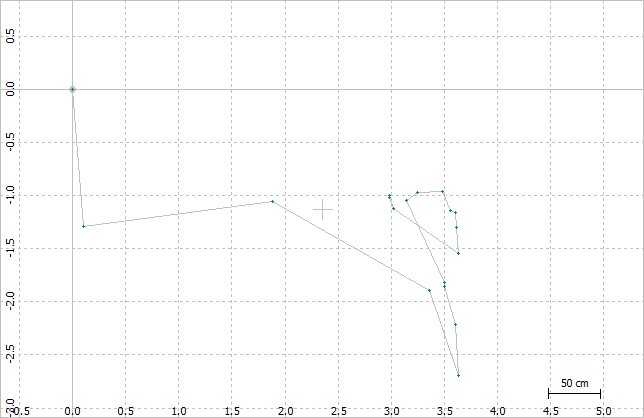
On voit très clairement l'impact de la correction liée à la double fréquence, qui permet de réduire l'erreur de plusieurs mètres à quelques dizaines de centimètres.
Dilution géométrique
Outils : https://gnssplanning.com, calcul le GDOP.
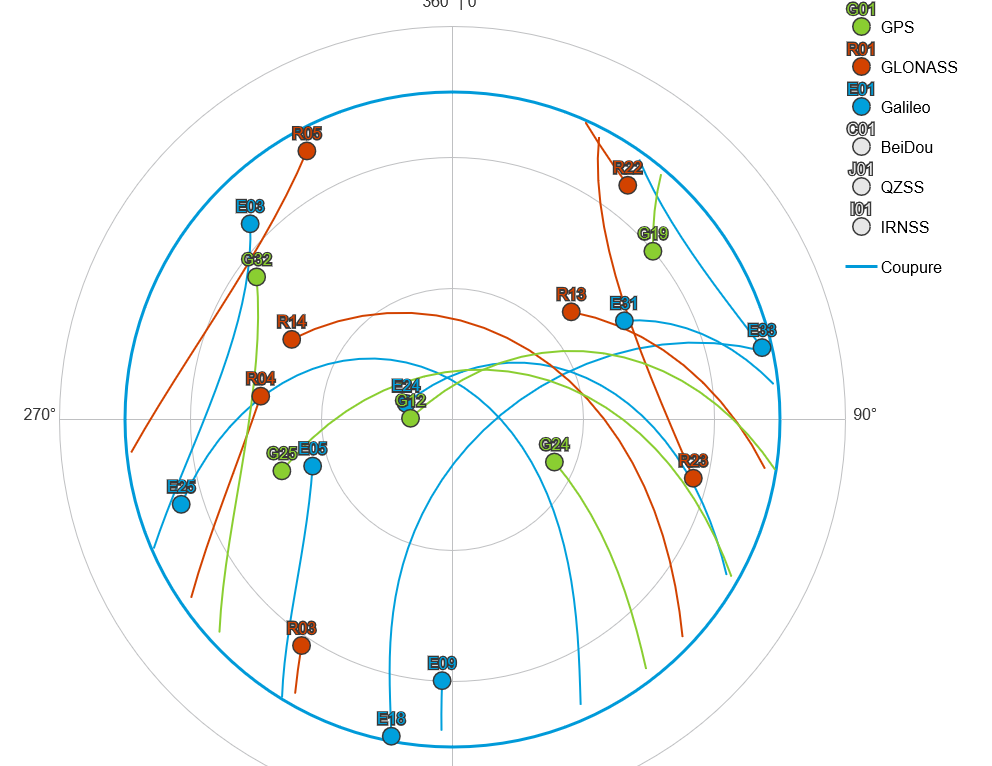
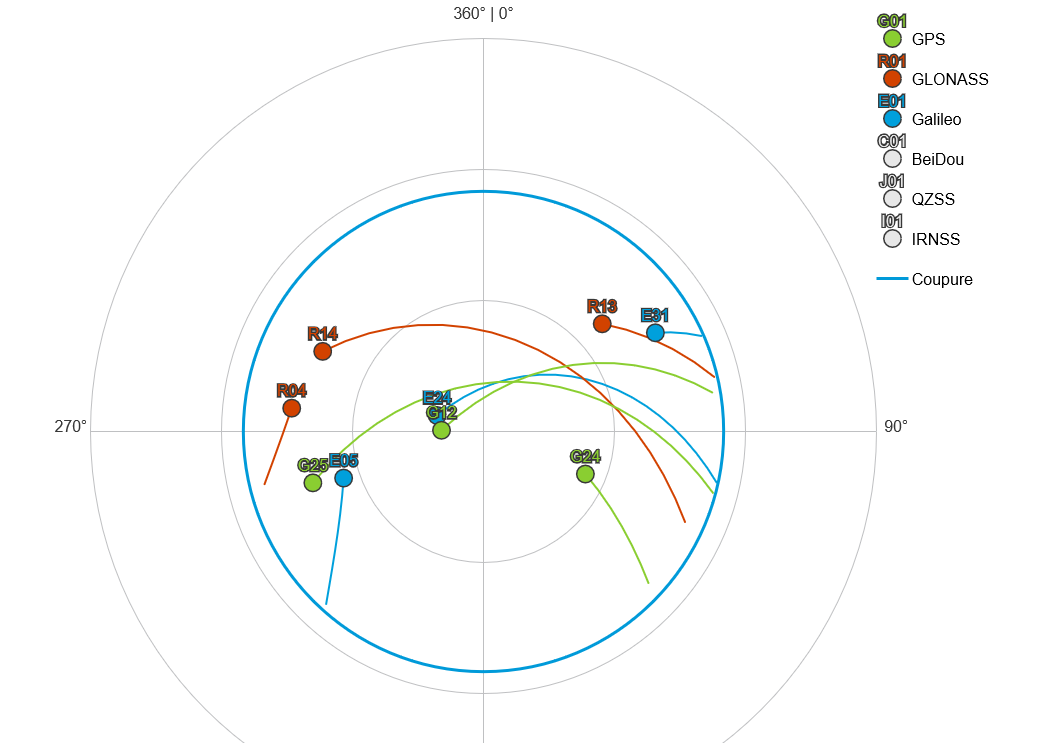
Expérimentations
Calcul de la position à l’aide de RTKlib avec un mask de 15° et 35°.
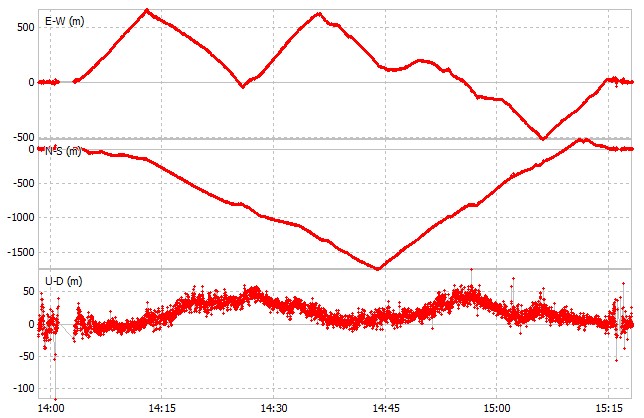
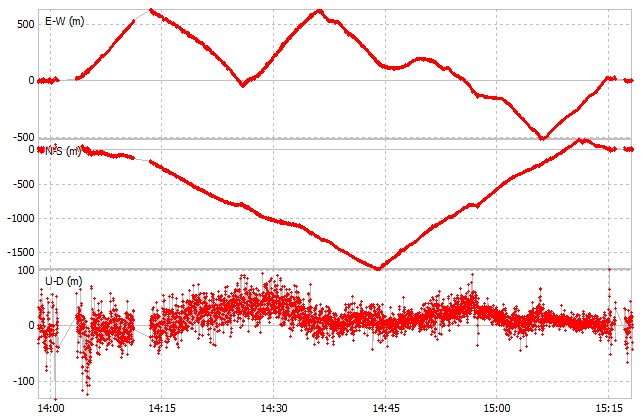
On remarque que le GDOP est plus élevé avec un mask de 35°, ce qui entraîne une plus grande erreur de positionnement.
Cela est dû à la géométrie des satellites, qui influe sur la précision de la géolocalisation.
Conlusion
Les smartphones multibandes, multi-constellation permettent d’améliorer la précision de la position:
-
Une correction de l’erreur ionosphérique.
-
En ville, grâce à la réduction du multipath.
-
Le multi-constellation augmente le nombre de satellites utilisables, réduisant le GDOP.
Application commerciale possible : projet FLAMMINGO.
Perspectives : Solution RTK, PPP et augmenté par SBAS. (Voir début d’analyse dynamique en annexe)
Annexe 1
Élévation et SNR, impact sur la précision de la géolocalisation; On une tendance à avoir une meilleure précision lorsque l'élévation est plus élevée, et le SNR plus important.
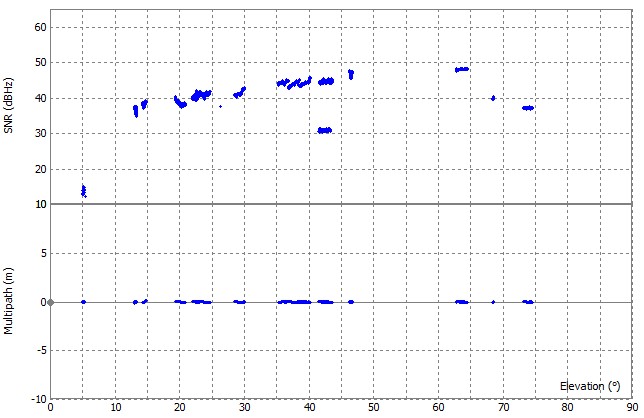
Annexe 2
Démonstration TEC
Modélisation de l’onde par:
$\vec{\underline{E}} = \vec{\underline{E_0}} \cdot exp(i(\omega t - kx))$
Hypothèses :
Poids et champ magnétique négligeable devant le champ électrique.
PDF et passage en complexe :
$m_e \frac{d \vec{\underline{v_e}}}{dt} = -e \vec{\underline{E}} \leftrightarrow i m_e \omega \vec{\underline{v_e}} = -e \vec{\underline{E}}$
Par définition : $\vec{\underline{j_e}}= -e n_e \vec{\underline{v_e}}$,
soit:
$\vec{\underline{j_e}} = \frac{e^2 n_e}{i m_e \omega} \vec{\underline{E}}$
D’après l’équation de propagation :
$\vec{\Delta} \vec E - \frac{1}{c^2} \frac{\partial^2 \vec E}{\partial t^2} = \mu_0 \frac{\partial \vec j}{\partial t}$
On en déduit le signal complexe :
$k^2 = \frac{\omega^2}{c^2} - \frac{e^2 n_e}{c^2 \epsilon_0 m_e}$
Vitesse de phase :
$v_{\phi} = \frac{\omega}{k} = \frac{c}{\sqrt{1 - \frac{{f_p}^2}{f^2}}}$
L’erreur de distance: $L_1=c \tau_1$
Le retard:
$\tau=\int_{0}^{H} \frac{dz}{v_g} - \int_{0}^{H} \frac{dz}{c}$
Ainsi le retard est : $ \boxed{\frac{1}{c} \int_{0}^{H} (\frac{c}{v_g} - 1)} $
On a que $v_g=v_{\phi} \cdot (1-\frac{f_p^2}{f_1^2})$
Soit: $L_1=\frac{a}{f_1^2} C_{ET}$
On a donc :
$$ \boxed{C_{ET}=\int_{0}^{H}n_e dz = \frac{\tau}{a} \frac{f_1^2 f_5^2}{f_1^2 - f_5^2}} $$
D’après sujet E3A, (Polytech 2020)
Annexe 3
Le signal GPS
Les récepteurs génèrent les fréquences porteuses L1 et L5 et compare avec celui reçu :
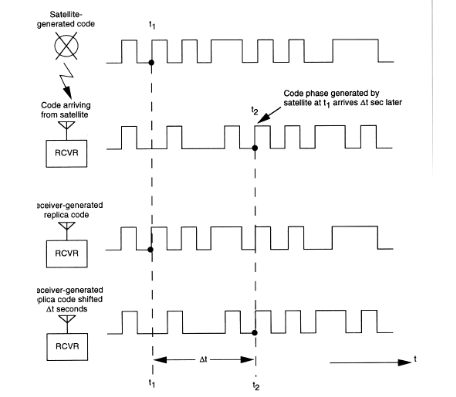
Détermine le pic de corrélation (code GOLD) et en déduit le décalage temporel.
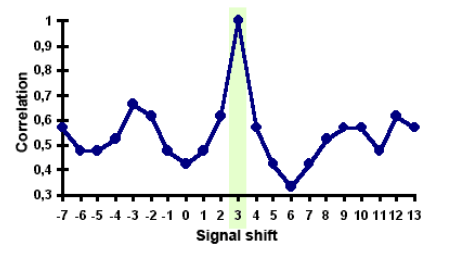
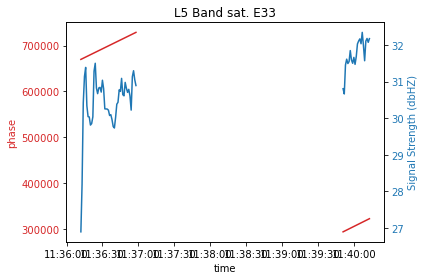
Duty-Cycle
Ainsi comme le récepteur ne connait que le nombre de phases, il l’initialise à chaque fois. Lorsque qu’il y a une interruption de signal, un nouveau cycle recommence.
Annexe 4
Démonstration Multipath
On modélise les signaux $L_1$ et $L_5$ par:
$P_1 = R +I1 +MP1$ et $P_5 = R + I5 + MP5$
Avec : $R$ la distance réelle, $I1$ et $I5$ les erreurs ionosphériques,
$MP1$ et $MP5$ les erreurs multipath.
Ainsi que leurs phases respectives :
$L_1 = R - I1 + mp1 + B1$ et $L_5 = R - I5 + mp5 + B5$
Avec : $B1$ et $B5$ les ambiguïtés de phase. On néglige
$mp << MP \leftrightarrow mp=0$
D’après Annexe 3 $I_i = \frac{A}{f_i^2}T_{EC}$ soit:
$$ \frac{I_5}{I_2} = \frac{f_1}{f_5}^2 = \alpha $$
Après calcul des différentes combinaisons, on obtient :
$MP1 - P1 + (\frac{2}{\alpha - 1} + 1)L1 - (\frac{2}{\alpha - 1}) L5 = cte$
Comme le multipath est à valeur moyenne nulle, on a : $\boxed{MP1 = P1 - (\frac{2}{\alpha - 1} + 1)L1 + (\frac{2}{\alpha - 1}) L5}$
De même pour $MP5$ : $$ \boxed{MP5 = P5 - (\frac{2 \alpha}{\alpha - 1})L1 + (\frac{2 \alpha}{\alpha - 1} - 1)L5} $$
D’après Eric Calais, (Calais, n.d.)
Atténuation du multipath
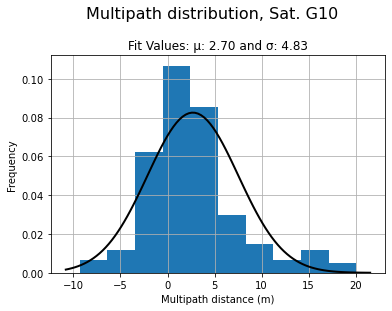
Annexe 5
Fichiers RINEX
RINEX : Receiver Independent Exchange Format
Fichier d’observation :
- Phase
- Code (Pseudorange)
- Doppler
- Rapport signal sur bruit (C/N0)
Fichier de navigation :
- Ephémérides
- Heure
- Erreurs ionosphériques
- Erreurs de relativité restreinte
- ...
Exemple de fichier RINEX
Fichier de navigation :
2 NAVIGATION DATA RINEX VERSION / TYPE
CCRINEXN V1.6.0 UX CDDIS 17-JAN-23 13:53 PGM / RUN BY / DATE
IGS BROADCAST EPHEMERIS FILE COMMENT
0.2980D-07 0.2980D-07 -0.1192D-06 0.0000D+00 ION ALPHA
0.1516D+06 -0.1638D+06 0.0000D+00 0.6554D+05 ION BETA
-0.558793544769D-08-0.177635683940D-13 405504 2245 DELTA-UTC: A0,A1,T,W
18 LEAP SECONDS
END OF HEADER
1 23 1 17 0 0 0.0 0.223558396101D-03-0.466116034659D-11 0.000000000000D+00
0.850000000000D+02-0.782812500000D+02 0.394659296287D-08 0.400711955078D+00
-0.396929681301D-05 0.122224817751D-01 0.587478280067D-05 0.515365424919D+04
0.172800000000D+06-0.124797224999D-06-0.163560063383D+01 0.128522515297D-06
0.989089047026D+00 0.281125000000D+03 0.937393524649D+00-0.806640742682D-08
-0.222509268404D-09 0.100000000000D+01 0.224500000000D+04 0.000000000000D+00
0.200000000000D+01 0.000000000000D+00 0.465661287308D-08 0.850000000000D+02
0.165673000000D+06 0.400000000000D+01 0.000000000000D+00 0.000000000000D+00
2 23 1 17 0 0 0.0-0.626868102699D-03 0.227373675443D-11 0.000000000000D+00
0.780000000000D+02-0.814375000000D+02 0.447197198987D-08-0.574309133343D+00
-0.426545739174D-05 0.200936053880D-01 0.661425292492D-05 0.515369303703D+04
Fichier d’observation :
3.03 OBSERVATION DATA M RINEX VERSION / TYPE
GnssLogger Xiaomi 10 20230117 132006 UTC PGM / RUN BY / DATE
Google GnssLogger MARKER NAME
G 8 C1C L1C D1C S1C C5Q L5Q D5Q S5Q SYS / #### / OBS TYPES
E 8 C1C L1C D1C S1C C5Q L5Q D5Q S5Q SYS / #### / OBS TYPES
E L5Q 0.00000 SYS / PHASE SHIFT
C1C 0.000 C1P 0.000 C2C 0.000 C2P 0.000 GLONASS COD/PHS/BIS
END OF HEADER
> 2023 01 17 13 20 06.9995244 0 28
G06 -9106.87612 2273.16912 13.59612 -6784.17911 1726.83711 11.19011
G10 8004.38113 -2010.76113 19.12713 5935.91711 -1433.92611 10.63511
G11 -12882.26412 3222.43712 17.30012
G12 20136967.66714 -2423.03914 846.72914 28.16814
G15 14170.13812 -3560.32412 15.63512
G17 11523.98012 -2880.99612 16.73612
Note : Les données ont été tronquées pour des raisons de lisibilité. Dataset complet : https://mega.nz/folder/dlRWAb5K#JNMzol3-uhl9gx0fF0147w
Annexe 6
Biais d’horloge - Xiaomi Mi 8
Exemple de biais d’horloge et de fréquence pour un récepteur Xiaomi Mi 8, expérimental.
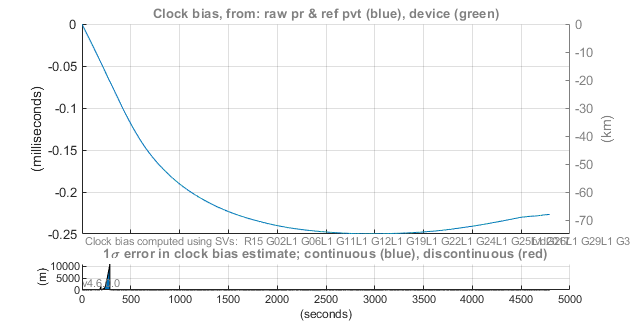
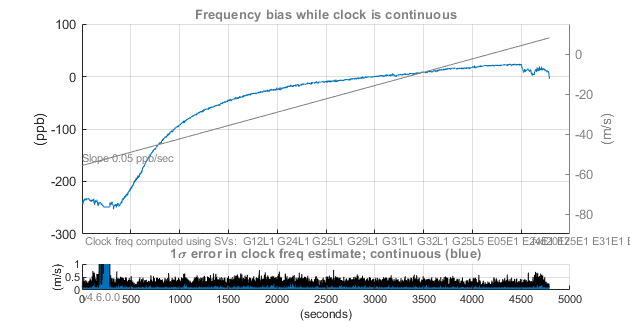
Annexe 7
Code python - COMPACT3
import pandas as pd
from datetime import datetime, timedelta
nbval=0
sat=[]
def compread(filepath):
file = open(filepath, "r")
line = file.readline()
i=1
time=0
cellsat=[]
value=[]
output=[['TIME', 'PRN', 'misure']]
while line:
if "GPS_START_TIME" in line:
celldata=line.split()
year=int(celldata[1])
month=int(celldata[2])
day=int(celldata[3])
hour=int(celldata[4])
minute=int(celldata[5])
second=int(float(celldata[6]))
dt=datetime(year, month, day, hour, minute, second)
if (i % 2) != 0 and i>2:
cellsat=line.split()
time=int(float(cellsat[0]))
if int(cellsat[1]) != -1:
nbval=int(cellsat[1])
sat=[cellsat[e] for e in range(2,nbval+2)]
if (i % 2) == 0 and i>2:
cellval=line.split()
value=[]
for f in range(nbval):
if "S" in cellval[f]:
value.append("NaN")
else:
value.append(float(cellval[f]))
output.append([(dt+timedelta(seconds=time)),sat[f],value[f]])
i=i+1
line = file.readline()
file.close()
return pd.DataFrame(output[1:], columns=output[0])
Code complet : https://github.com/n005/tipe
Annexe 8
Étude dynamique
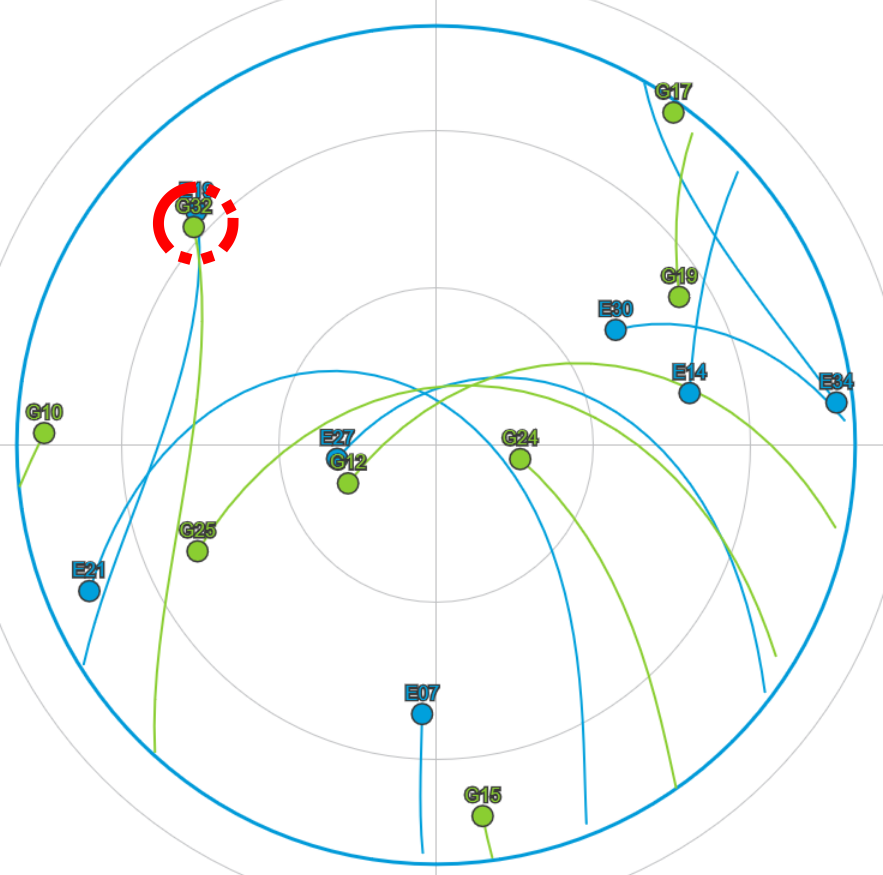
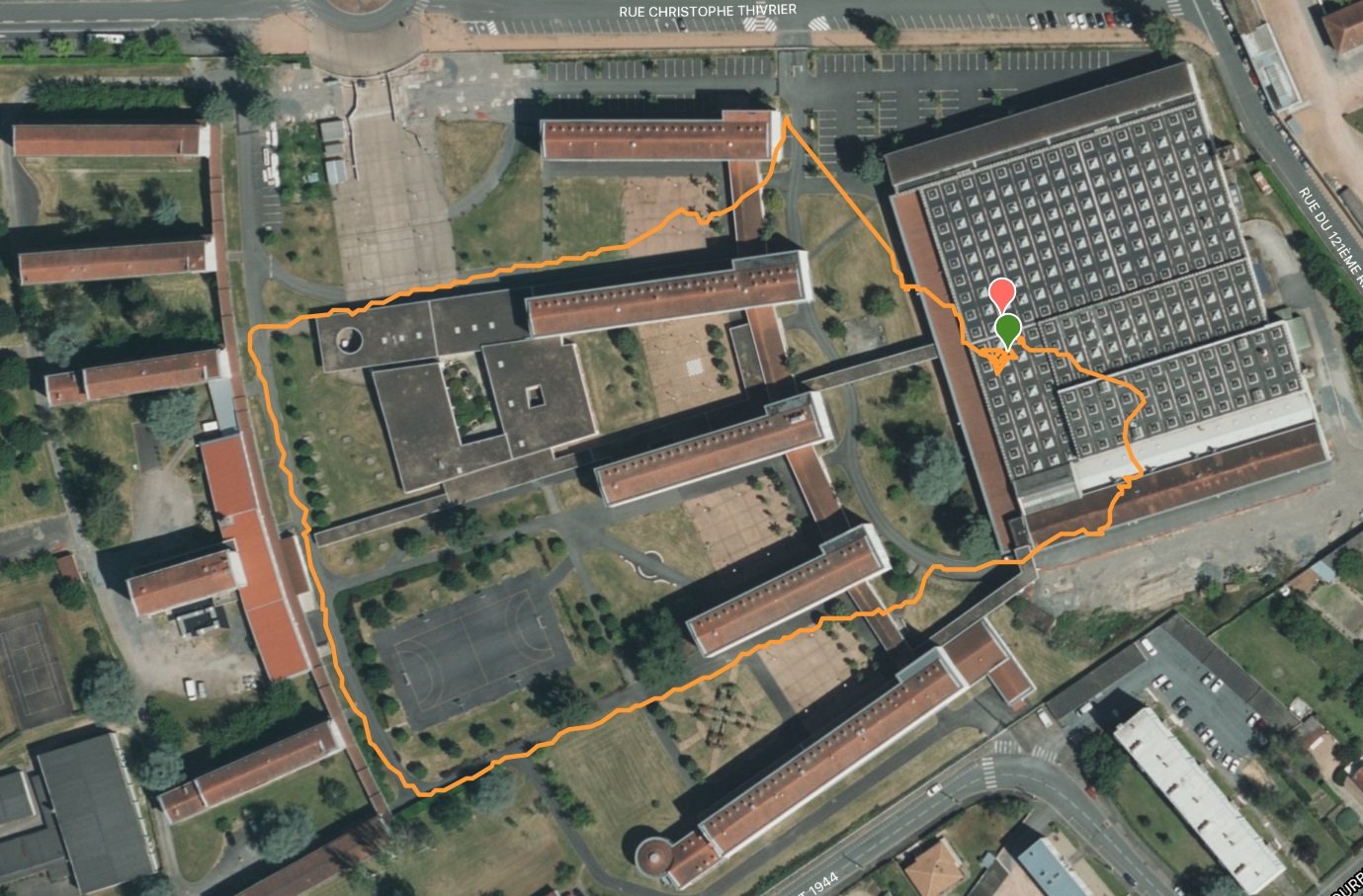
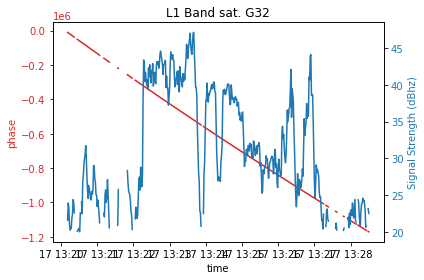
Comparaison
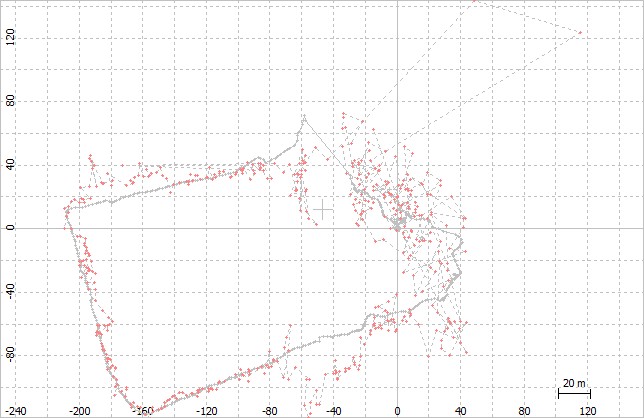
Réseau Centipede
Réseau RTK, permettant de faire du positionnement RTK (Real Time Kinematic, Cinématique temps réel) et DGNSS(GNSS différentiel).

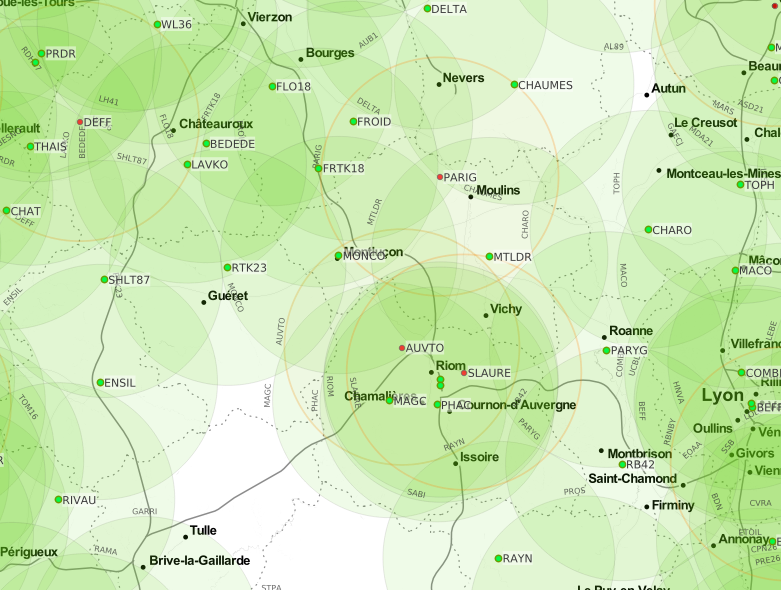
Utilisation de RTKlib permettant de récupérer les données.
Annexe 9
Outils - RTKlib
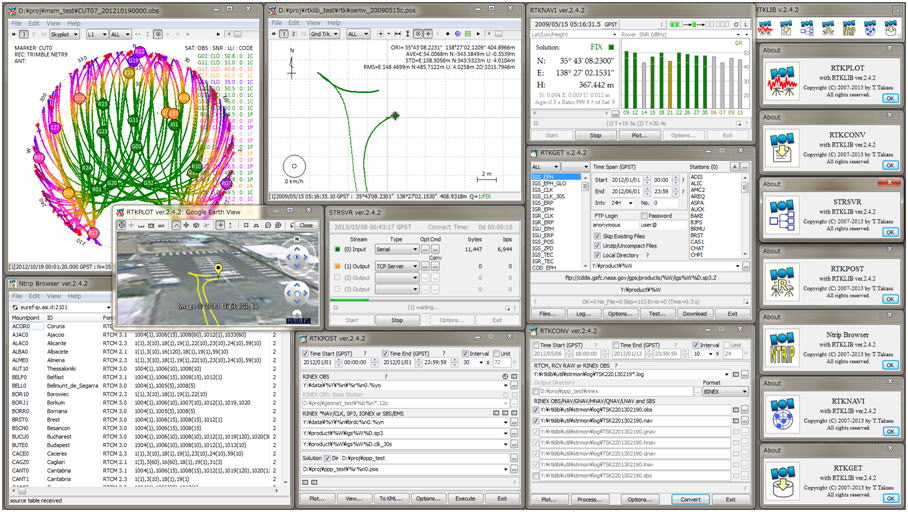
Outils - GnssLogger
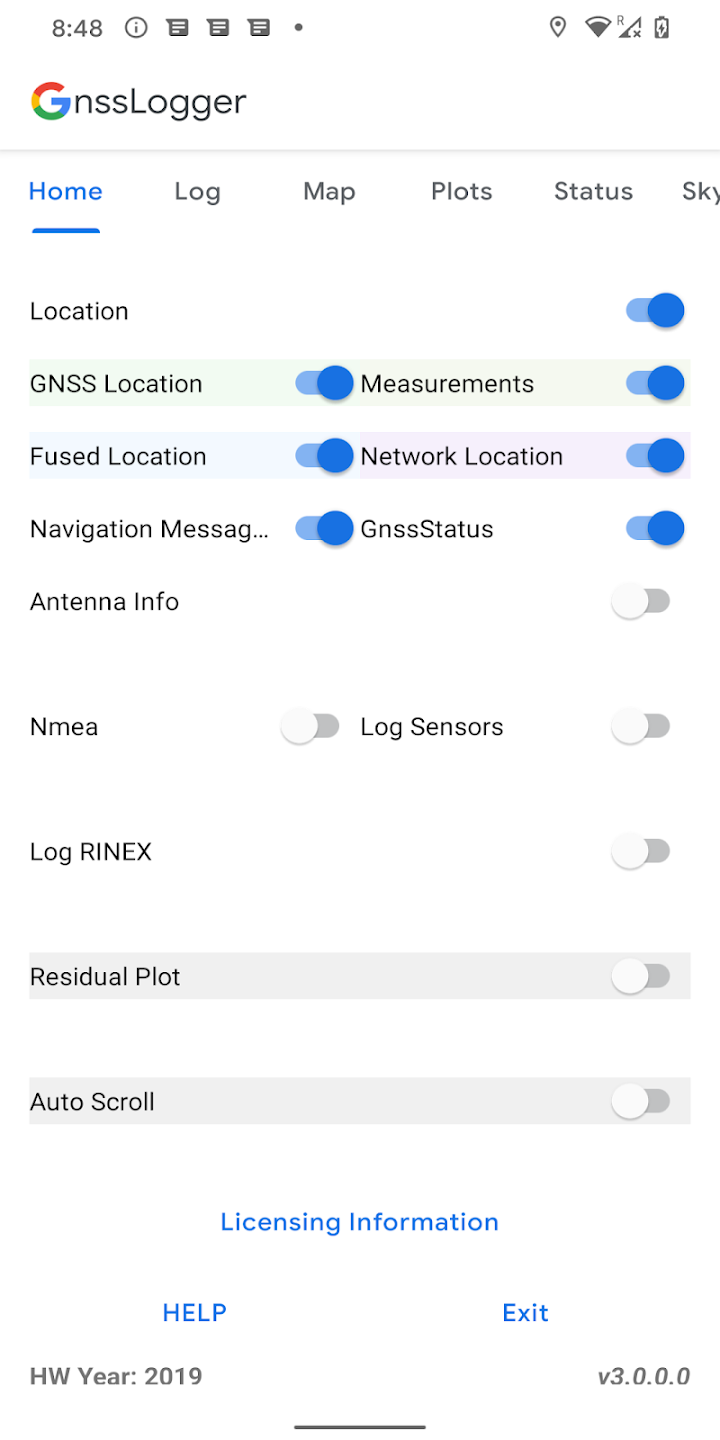
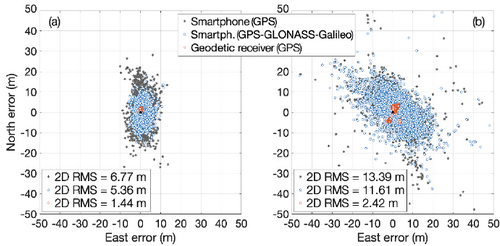
Annexe 10
Comparaison Ville-campagne Résultats issue de l’étude de (Robustelli, Baiocchi, and Pugliano 2019)
Références
- Calais, Eric. n.d. “Géopositionnement GNSS, Principe Et Applications.” https://www.geologie.ens.fr/~ecalais/teaching.
- ESA. n.d.a. “ESA GNSS Navipedia.” https://gssc.esa.int.
- . n.d.b. “GNSS Market Report.” https://gssc.esa.int/navipedia/index.php/GNSS_Market_Report#Report_Overview.
- Gillies, Robert. 2006. “Modelling of Transionospheric HF Radio Wave Propagation for the ISIS II and ePOP Satellites,” January.
- GPS.gov. n.d. “GPS Constellation.” https://www.gps.gov/multimedia/images/constellation.jpg.
- Polytech, E3A -. 2020. “Épreuve de Physique.”
- Robustelli, Umberto, Valerio Baiocchi, and Giovanni Pugliano. 2019. “Assessment of Dual Frequency GNSS Observations from a Xiaomi Mi 8 Android Smartphone and Positioning Performance Analysis.” Electronics 8 (January). https://doi.org/10.3390/electronics8010091.
- Serrano, Luis, Don Kim, and Richard B. Langley. 2008. “Carrier-Phase Multipath Calibration in GPS-RTK Machine-Guidance Applications.” In 2008 IEEE/ION Position, Location and Navigation Symposium, 479–88. https://doi.org/10.1109/PLANS.2008.4570023
- University Corporation for Atmospheric Research, Randy Russell. n.d. “Regions of the Ionosphere, Showing the d, e, and f Layers.” https://scied.ucar.edu/learning-zone/atmosphere/ionosphere.
- Xue, Zhihao, Zukun Lu, Zhibin Xiao, Jie Song, and Shaojie Ni. 2022. “Overview of Multipath Mitigation Technology in Global Navigation Satellite System.” Frontiers in Physics 10. https://doi.org/10.3389/fphy.2022.1071539.